19.单目测距原理介绍

根据相机成像的原理，在满足一定约束条件下，理论上是可以根据目标点的像素坐标计算出其对应的深度信息的。

相机成像模型的再次介绍

根据,

1.基本相机模型及参数 (opens new window)

2.OpenCV相机标定 (opens new window)

这两部分的介绍，我们可以知道相机的基本模型，其原理本质上还是小孔成像，感光芯片记录下成像信息变成图片来实现的。

现在我们来看下OpenCV相机标定的结果，为了简化介绍，畸变系数这里不再重复介绍，可以参考上面两个博客。

相机标定的内参矩阵为:

$$\left[\begin{array}{ccc}{f}_x& 0.& c_x\\ 0& f_y& c_y\\ 0& 0.& 1\end{array}\right]=\left[\begin{array}{ccc}1044.43& 0.& 959.5\\ 0& 1047.87& 541.5\\ 0& 0.& 1\end{array}\right]$$

相机原始分辨率为：WxH=1920x1080

相机的焦距为2.93mm

相机的感光芯片上像元大小是=2.8umx2.8um

根据相机内参的公式：，在这里其中是像元的大小，是焦距，因此这和上面标定的结果1044.43/1047.87十分接近，这也验证了相机模型的正确性。

单目测距的几何原理

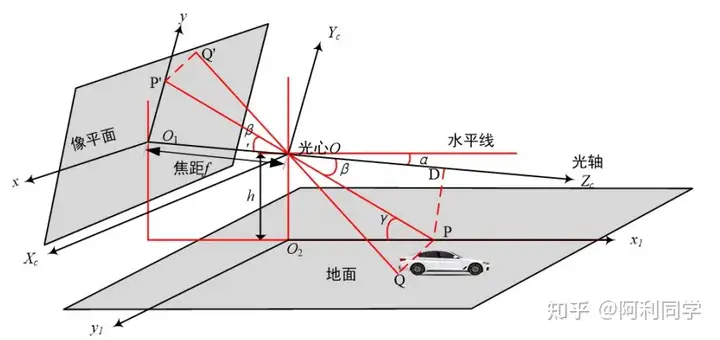
单目测距的几何原理可以借用下面这张图来做介绍：

reference:
https://zhuanlan.zhihu.com/p/664389534 (opens new window)

参考上图：

像平面是相机的成像平面，也就是感光芯片所在的平面。

光心O处的坐标系{C}是相机所在的坐标系，点，点和点Z_c共线，线是相机的主轴，相机安装时有一定的俯仰角，因此相机主轴和水平线的夹较为

相机的光心到待测对像所在平面的垂直高度为，记为

在点沿相机坐标系的X轴Y轴在待测对像所在平面建立坐标系

待测对像上的目标点为，其在像平面上的成像点为，记其在坐标系中的坐标为，在图像上的像素坐标为

目标点Q向坐标系的X轴做垂线，得点P,连接OP其和像平面的Y轴交于点,同时点也是到像平面Y轴的垂足。

记为，作为其对角也为,从图上看以看出

角很容易求出：

$$\begin{gathered} \beta =arctan\frac{P^{\prime }{O}_1}{O_{1}O} \\ \beta =arctan\frac{(c_y-v)\ast d_y}{f} \end{gathered}$$

求得后可得，由此即目标点在轴上的距离为:

$$P{O}_2=\frac{h}{tan\gamma }$$

以上就求出了目标点Q在坐标系上X轴上的坐标。

再来看Y轴上的坐标:

根据三角形相似于三角形，容易求得PQ的长度为：

$$PQ=\frac{(u-cx)\ast d_x\ast \sqrt{h^2+P{O}_2^2}}{\sqrt{[(cy-v)\ast d_y{]}^2+f^2}}$$

如上，就可以求出目标点Q在坐标系上Y轴上的坐标。

值得注意的是：

• 以上仅考虑了投影点出现在图像平面第二象限的情况，如果目标点在图像平面的第三/四象限，还需对计算结果符号进行调整。

• 计算中涉及到除法，还需考虑除以零的情况。

reference

• 1.https://zhuanlan.zhihu.com/p/664389534 (opens new window)
• 2.https://zhuanlan.zhihu.com/p/24651968 (opens new window)