# 1.Introduction
Rapid Object Detection using a Boosted Cascade of Simple Features (opens new window)
Haar特征是由Viola和Jones在2001年提出的,用于面部识别和人脸检测。
Haar特征的基本思想是将图像划分为多个矩形区域,并计算每个矩形区域内像素值的差异,从而得到一组能够有效描述图像特征的数值。Haar特征与小波变换有相似之处,因此也被称之为Haar小波。
Haar特征由一系列可以缩放的矩形(如下图所示)结合原图像进行运算得到的,这种方法最早在1909年由匈牙利数学家Alfred Haar提出。Haar Feature的求解过程与卷积有相似之处。

如上图中,一种矩形表示一种Haar特征,大小不同也能得到不同的Haar特征。其应用思路如下,考虑人脸检测,Haar特征能够识别出人脸的关键部位。如下图,检测眉毛位置使用图中所示意的Haar特征,因眉毛处的像素比额头处要暗,也就是灰度值小,拿矩形白色部分的像素和减去黑色矩形的像素和,能得到比其他部位更大的灰度插值。同样,对鼻子处,左右部分也存在灰度差值。
图片来自于1 (opens new window)

# 2.Haar特征计算详解

以上图所示的模式来计算Haar特征。
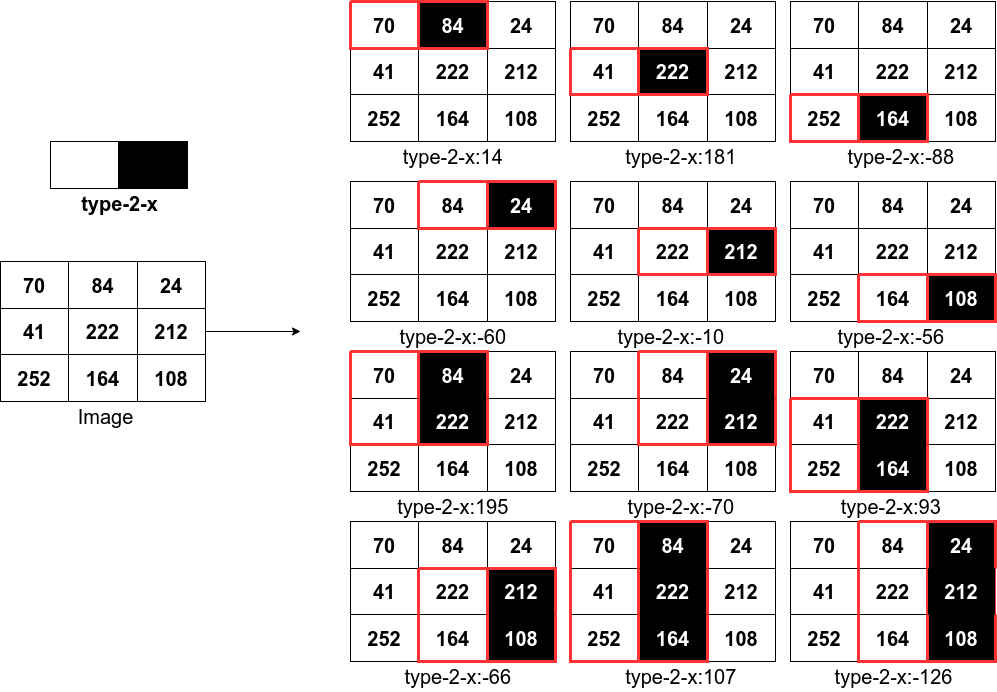
上面这个图表示的是对一个3x3大小的图像求type-2-x模式的Haar特征的过程,即黑色区域像素和减去白色区域像素和。一个宽高3x3的图像,经过rescale的type-2-x的Haar变换可以得到12个特征值。当图像尺度变大时能够得到更多的Haar特征。对一个宽高8x8的图像,type-2-x的Haar变换可以得到576个特征值;而对一个宽高56x56的图像,type-2-x的Haar变换可以得到1251264个特征值。
从上面的示例中也可以看到,Haar变换的计算过程涉及到图像区域像素的求和,不同scale的Haar变换,图像区域其实是有重和的,反复的进行求和比较耗时,为了提高计算的性能,可以使用积分图改进Haar算法。
**积分图的定义是对于图像每个像素将其左上角所有像素求和所得。**如上面的宽高3x3图像的示例,其对应的积分图为:
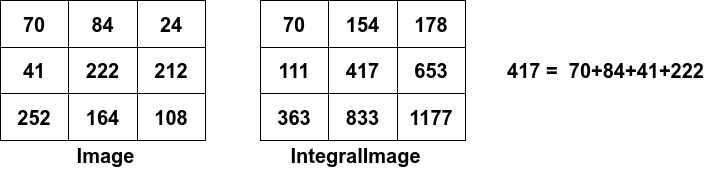
有了积分图后,可以借助积分图求图像特定区域的面积。
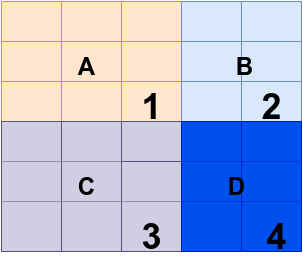
看上面这张图,表示原始图像的积分图,想要求原图像区域D中的像素和,使用积分图计算如下:
积分图上点1处的值为:ii(1)=RectSum(A)
积分图上点2处的值为:ii(2)=RectSum(A) - RectSum(B)
积分图上点3处的值为:ii(3)=RectSum(A) + RectSum(C)
积分图上点4处的值为:ii(1)=RectSum(A) - RectSum(B) + RectSum(C) + RectSum(D)
求区域D的像素和可表示成RectSum(D)=ii(4) + ii(1) - ii(2) - ii(3),通过这种方式计算原图像中区域像素的和可以极大的减少运算量,加快运算速度。
通过上面的介绍可以知道,一张图像可以得到非常多的Haar特征,很多特征都是和目标检测无关的,传统的方法通常将Adaboost分类器和Haar特征一起使用,其思想是将Haar特征当成很多个弱分类器,再使用Adaboost将如此多的弱分类器组合到一起组成强分类器。实际使用中,采用级联的分类器,以便更快的判断出图像区域中是否包含人脸,如下图,

使用Adaboost和Haar特征来做人脸检测的例子可以参考SkImage (opens new window)的示例。
# 3.使用sklearn计算Haar特征
skimage.feature.haar_like_feature(int_image, r, c, width, height, feature_type=None, feature_coord=None)
r: 计算Haar特征图像的起始区域左上角的行坐标c: 计算Haar特征图像的起始区域左上角的列坐标width: 计算Haar特征图像的区域宽度height: 计算Haar特征图像的起始区域高度feature_type:计算Haar特征使用的模式,支持type-2-x/type-2-y/type-3-x/type-3-y/type-4这几种。feature_coord:计算Haar特征使用的模式矩形,白色和黑色区域的起始和终止坐标,其值可以使用haar_like_feature_coord()方法来获取。具体看下面的例子。

from skimage import feature
import numpy as np
from skimage.transform import integral_image
img = np.random.randint(0, 255, (56, 56))
img = np.uint8(img)
"""
img:
[[ 70 84 24]
[ 41 222 212]
[252 164 108]]
"""
types = np.array(['type-2-x', 'type-2-x'])
int_image = img
h, w = int_image.shape[:2]
ii = integral_image(int_image)
feat_coord = np.array([[[[0, 0], [0, 0]], [(0, 1), (0, 1)]],[[(0, 0), (1, 0)], [(0, 1), (1, 1)]]])
feat = feature.haar_like_feature(ii, 0, 0, w, h, feature_type=types, feature_coord=feat_coord)
"""
intergral_img:
[[ 70 154 178]
[ 111 417 653]
[ 363 833 1177]]
Haar Feature: [ 14 195]
使用haar_like_feature_coord计算矩形的起始区域:
feat_coord, feat_type = feature.haar_like_feature_coord(3, 3, 'type-2-x')
print(feat_coord)
"""
Haar Coordinate:
[list([[(0, 0), (0, 0)], [(0, 1), (0, 1)]])
list([[(0, 0), (1, 0)], [(0, 1), (1, 1)]])
list([[(0, 0), (2, 0)], [(0, 1), (2, 1)]])
list([[(0, 1), (0, 1)], [(0, 2), (0, 2)]])
list([[(0, 1), (1, 1)], [(0, 2), (1, 2)]])
list([[(0, 1), (2, 1)], [(0, 2), (2, 2)]])
list([[(1, 0), (1, 0)], [(1, 1), (1, 1)]])
list([[(1, 0), (2, 0)], [(1, 1), (2, 1)]])
list([[(1, 1), (1, 1)], [(1, 2), (1, 2)]])
list([[(1, 1), (2, 1)], [(1, 2), (2, 2)]])
list([[(2, 0), (2, 0)], [(2, 1), (2, 1)]])
list([[(2, 1), (2, 1)], [(2, 2), (2, 2)]])]
"""