使用矩阵计算卷积

GEMM算法

矩阵乘法运算(General Matrix Multiplication)，形如：

$$C=AB,A\in {\mathbb{R}}^{m\times k},B\in {\mathbb{R}}^{k\times n},C\in {\mathbb{R}}^{m\times n}$$

矩阵乘法的计算可以写成如下公式：

$$C_{m,n}=\sum _{k=1}^K{A}_{m,k}{B}_{k,n};m,n,k\in \mathbb{R}$$

矩阵的乘法操作可以写成如下图所示，

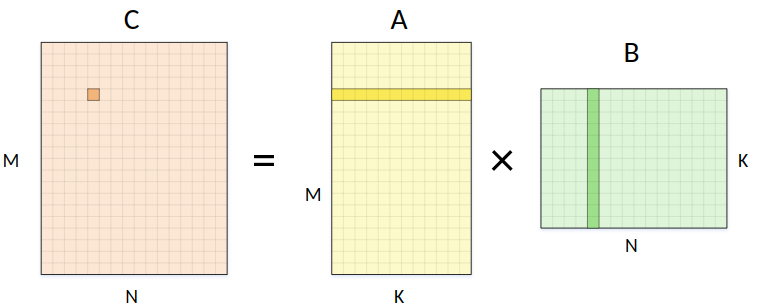
写成伪代码的形式为：

for i=1 to n
   for j=1 to n    
     c[i][j]=0
     for k=1 to n
         c[i][j] = c[i][j]+a[i][k]*b[k][j]

从上面可以看到使用普通的矩阵乘法运算，其复杂度是，这个复杂度相对来说是很高的，当矩阵的维度很大时，运算量会显著增加。

矩阵运算作为基础运算，有大量的科学家对其进行研究，试图降低其运算复杂度。

以Strassen’s Matrix Multiplication Algorithm为例，其将矩阵乘法的运算复杂度降低到了。

这个算法是Strassen于1969年发布的论文《Gaussian Elimination is not Optimal. (opens new window)》中提出的,主要是通过矩阵块的操作，减少乘法运算的次数。

将矩阵写成矩阵块的形式：

$$A=\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right),B=\left(\begin{array}{cc}{B}_{11}& B_{12}\\ B_{21}& B_{22}\end{array}\right),C=\left(\begin{array}{cc}{C}_{11}& C_{12}\\ C_{21}& C_{22}\end{array}\right)$$

由,可得：

$$\begin{array}{c}{C}_{11}=A_{11}{B}_{11}+A_{12}{B}_{21}\\ C_{12}=A_{11}{B}_{12}+A_{12}{B}_{22}\\ C_{21}=A_{21}{B}_{11}+A_{22}{B}_{21}\\ C_{22}=A_{21}{B}_{12}+A_{22}{B}_{22}\end{array}$$

写成上面的形式，只是把矩阵的乘法写成了块的运算，并没能改变乘法的次数，除了分块可以在硬件上实现并行运算，并没有改变算法本身的复杂度。

Strassen将矩阵的运算写成如下形式，

$$\begin{array}{rl}{M}_1& =(A_{11}+A_{22})(B_{11}+B_{22})\\ M_2& =(A_{21}+A_{22})B_{11}\\ M_3& =A_{11}(B_{12}-B_{22})\\ M_4& =A_{22}(B_{21}-B_{11})\\ M_5& =(A_{11}+A_{12})B_{22}\\ M_6& =(A_{21}-A_{11})(B_{11}+B_{12})\\ M_7& =(A_{12}-A_{22})(B_{21}+B_{22})\end{array}$$$$\begin{array}{rl}{C}_{11}& =M_1+M_4-M_5+M_7\\ C_{12}& =M_3+M_5\\ C_{21}& =M_2+M_4\\ C_{22}& =M_1-M_2+M_3+M_6\end{array}$$

从上面这11个公式中可以看到，一次分治后降低到了7次乘法运算，相较于原来的8次少了一次，可以证明，这样可以将矩阵的乘法复杂度降低到。

在此之后1990年Coppersmith和Winograd合作提出的Coppersmith–Winograd算法将复杂度降低到了,2014年斯坦福大学的Virginia Williams发表的论文Multiplying matrices in o(n2.373) time将复杂度降低到了，其演变过程如下图：

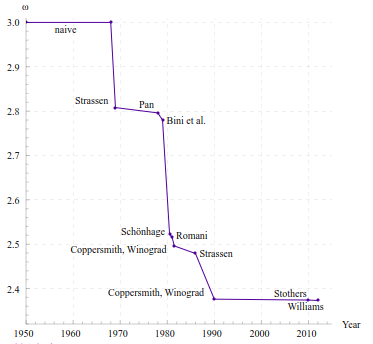
卷积运算

卷积运算的过程就是将卷积核在输入数据上滑动乘积求和的过程，其运算过程可以参考之前的文章

1.常规卷积神经网络 (opens new window)

其计算方式第一直观的想法肯定是根据卷积的定义，逐元素相乘求和，写成伪代码的形式如下：

input[C][H][W];
kernels[M][K][K][C];
output[M][H][W];
for h in 1 to H do
    for w in 1 to W do
        for o in 1 to M do
            sum = 0;
            for x in 1 to K do
                for y in 1 to K do
                    for i in 1 to C do
                    sum += input[i][h+y][w+x] * kernels[o][x][y][i];
         output[o][w][h] = sum;

这种方式落到了逐个元素的运算上，不利于对运算做优化，考虑第一部分对矩阵乘法运算优化的介绍，考虑能不能将卷积运算转换成矩阵乘法的运算呢？答案当然是可以。

这正是引入img2col算法的初衷，因为现在的GPU/CPU基本都有对矩阵运算加速的BLAS库(Basic Linear Algebra Subprograms)。

img2col的方法将卷积的输入和卷积核都转成了矩阵的形式，最后卷积的运算变成了矩阵的乘法，如此就可以使用矩阵的加速运算了。

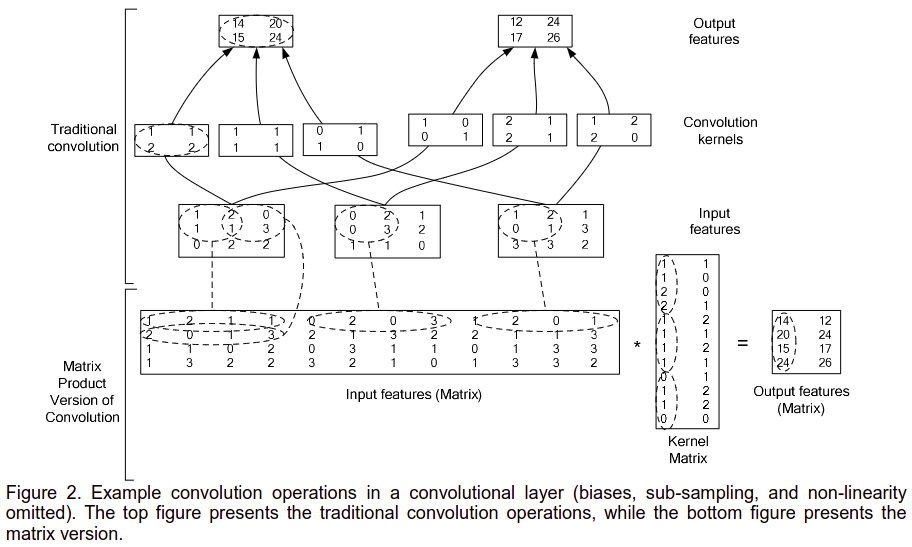
如上图，

输入是的图像

卷积核的大小为

卷积步长

输出的大小为

转换成矩阵乘法时，

输入数据转换成矩阵的

卷积核转换成矩阵的

使用乘法后得到的卷积运算的输出

可以看到，输出的矩阵，一列表示一幅卷积输出的图像，想比这是为什么称为img2col吧。

使用img2col实现卷积的代码如下：

int Conv2D::img2col(const std::vector<Eigen::MatrixXd> &x, std::vector<Eigen::MatrixXd> &out) const
{
    out.clear();
    assert(x.size() == channel_in_);
    int w_o = x[0].rows();
    int h_o = x[0].cols();
    w_o  = (w_o  - kernel_w_) / stride_ + 1;
    h_o = (h_o - kernel_h_) / stride_ + 1;
    Eigen::MatrixXd x_mat(w_o * h_o, kernel_w_ * kernel_h_ * channel_in_);
    for(int r = 0; r < h_o; ++r) {
        for(size_t c = 0; c < w_o; ++c) {
            for(size_t i = 0; i < channel_in_; ++i) {
                for(size_t h = 0; h < kernel_h_; h++) {
                    for(size_t w = 0; w < kernel_w_; w++) {
                        x_mat(r * w_o + c, i * kernel_h_ * kernel_w_ + h * kernel_w_ + w) 
                        = x[i](r * stride_ + h, c * stride_ + w);
                    }
                }
            }
        }
    }
    auto t1 = std::chrono::steady_clock::now();
    Eigen::MatrixXd res = x_mat * (*kernel_mat_);
    auto t2 = std::chrono::steady_clock::now();
    auto d = std::chrono::duration_cast<std::chrono::microseconds>(t2 - t1).count();
    std::cout << "img2col duration: " << d << "us" << std::endl;
    for(size_t i = 0; i < channel_out_; i++) {
        auto so = res.col(i);
        Eigen::MatrixXd m(h_o, w_o);
        for(int r = 0; r < h_o; ++r) {
            for(size_t c = 0; c < w_o; ++c) {
                m(r, c) = so(r * h_o + c);
            }
        }
        out.push_back(m);
    }
    return 0;
}

通过实验对比，img2col的方式比普通卷积的要快很多。

raw conv duration: 3530us
img2col duration: 260us

完整的实验代码可以参考仓库：

https://gitee.com/lx_r/basic_cplusplus_examples/tree/master/basic_cv (opens new window)

reference

• 1.https://stanford.edu/~rezab/classes/cme323/S16/notes/Lecture03/cme323_lec3.pdf (opens new window)
• 2.https://zhenhuaw.me/blog/2019/gemm-optimization.html (opens new window)
• 3.https://inria.hal.science/file/index/docid/112631/filename/p1038112283956.pdf (opens new window)