天天教程

# 局部二值模式LBP

# 1.基础介绍

局部二值模式（Local Binary Patterns，LBP）是一种用于图像处理和计算机视觉中的特征描述符。它通过将每个像素与其周围像素进行比较，并将结果编码为二进制数来描述图像的纹理信息。

LBP最初由芬兰奥卢大学的Timo Ojala、Matti Pietikainen和Topi Maenpaa于1994年在论文Multiresolution Gray-scale and Rotation Invariant Texture Classification with Local Binary Patterns (opens new window)中提出。他们提出了一种用于纹理分析和识别的算法，并将其应用于人脸识别任务。

LBP算法对于每个像素，将其与周围的8个像素进行比较，将比它亮的像素设为1，比它暗的像素设为0，这样就得到了一个8位二进制数。将这个二进制数转化为十进制数，得到的值即为该像素的LBP值。对于整张图像，可以统计不同LBP值的出现频率，并用这些频率作为图像的特征向量。

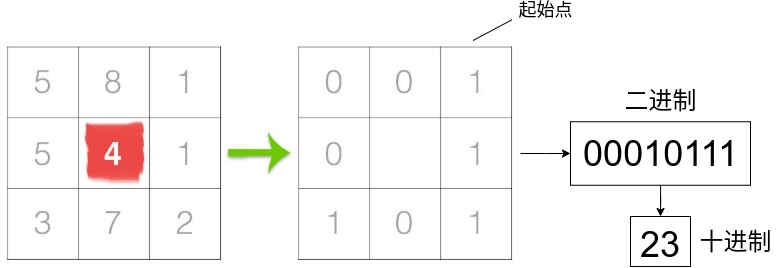
LBP算法具有计算简单、对光照变化不敏感、对噪声具有鲁棒性等优点，因此被广泛应用于图像处理和计算机视觉领域，如纹理分类、人脸识别、行人检测等。

# 2.局部二值模式（Local Binary Patterns，LBP）编码介绍

在上图中，展示了如何计算中心点的LBP编码，具体的如下：

图片来自于1

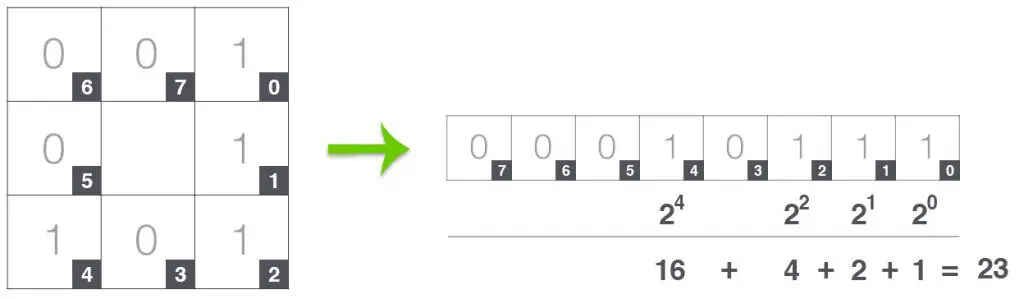
这里选右上角为起始点，沿顺时针方向，从由往左写出LBP的二进制编码，再转成十进制即可。逐像素将结果写到lbp对应的输出数组中，可以得到输出：

图片来自于1

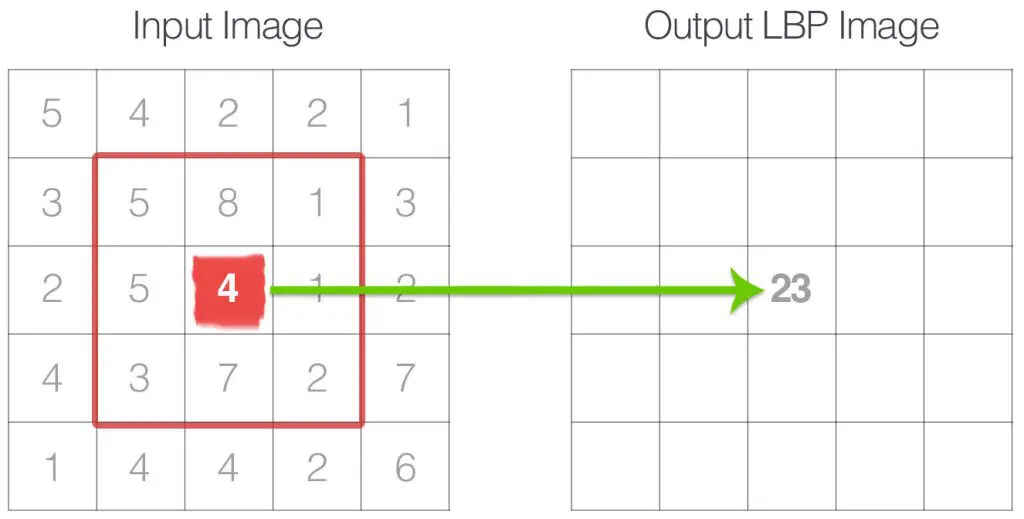
这里有三点值的注意，一个是LBP编码起始点的选择，另一个是可以选择邻近8个像素，也可以选半径为r圆上的点，最后一个是图像边界像素的处理。

  • 选半径为r圆上的点

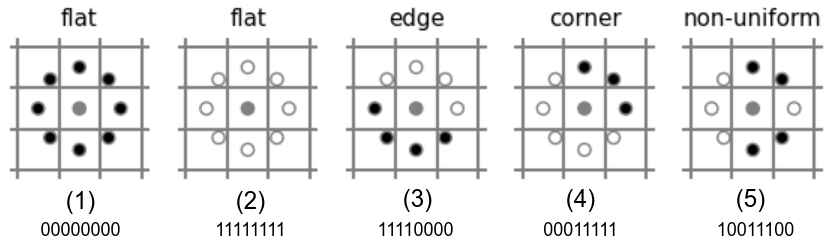
黑色的点表示像素值小于等于中心像素值，白色的点表示比中心像素值大。编码的起始位置为右侧中间的那个点。对于同一个算法实现，起始点只要保持一致就可以了，不同算法实现之间不具有可比性。

在LBP编码时，需要注意的是uniform和非uniform的编码方式，在LBP算法中，uniform是指具有最多两个跳变的二进制模式。例如，在8邻域中，二进制模式00011000、00010001、00001110等都是uniform模式，因为它们只有两个跳变。相反，二进制模式00011101、00100110等不是uniform模式，因为它们具有三个或更多的跳变。uniform LBP是指二进制编码中跳变次数不超过2次的LBP编码。因此，对于8邻域的LBP算法，有256种不同的二进制编码。其中，有59种uniform LBP编码，它们的跳变次数不超过2次。

对于图像分类等任务，使用uniform LBP特征可以减少非uniform LBP特征所引入的噪声，从而提高算法的准确性和稳健性。此外，由于uniform LBP特征的数量相对较少，因此计算速度也相对较快。

特别的，在skimage.feature.local_binary_pattern函数中实现的uniform模式和上面介绍的uniform还不一样，其只包含所有的1和0都是连续的且邻接的二进制码，对于8个邻近像素的模式，skimage.feature.local_binary_pattern的uniform编码只包括00000000/00000001/00000011/00000111/00001111/00011111/00111111/01111111/11111111这8种,其他形式的编码都是非uniform的。因此LBP码共有9个值。这种编码带有轮动性，对纹理的旋转有鲁棒性。

使用skimage计算lbp的简单示例如下,对于边界像素使用0值填充，

image = np.array([[5,4,2,2,1],[3,5,8,1,3],[2,5,4,1,2],[4,3,7,2,7],[1,4,4,2,6]], dtype=np.uint8)
radius = 1
n_points = 8
METHOD = "uniform"
lbp = skimage.feature.local_binary_pattern(image, n_points, radius, METHOD)
print(lbp)

计算过程：

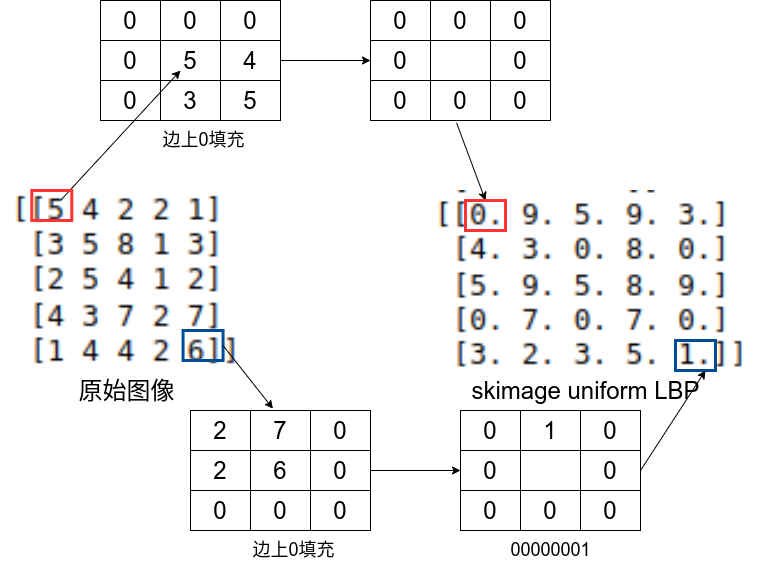
# 3.使用skimage求lbp

代码来自3

from skimage.transform import rotate
from skimage.feature import local_binary_pattern
from skimage import data
from skimage.color import label2rgb
import matplotlib.pyplot as plt
# settings for LBP
radius = 1
n_points = 8 * radius


def overlay_labels(image, lbp, labels):
    mask = np.logical_or.reduce([lbp == each for each in labels])
    return label2rgb(mask, image=image, bg_label=0, alpha=0.5)


def highlight_bars(bars, indexes):
    for i in indexes:
        bars[i].set_facecolor('r')


image = data.brick()
lbp = local_binary_pattern(image, n_points, radius, METHOD)


def hist(ax, lbp):
    n_bins = int(lbp.max() + 1)
    return ax.hist(lbp.ravel(), density=True, bins=n_bins, range=(0, n_bins),
                   facecolor='0.5')


# plot histograms of LBP of textures
fig, (ax_img, ax_hist) = plt.subplots(nrows=2, ncols=3, figsize=(9, 6))
plt.gray()

# 根据二进制编码划分边，平坦和角特征
titles = ('edge', 'flat', 'corner')
w = width = radius - 1
edge_labels = range(n_points // 2 - w, n_points // 2 + w + 1)
flat_labels = list(range(0, w + 1)) + list(range(n_points - w, n_points + 2))
i_14 = n_points // 4            # 1/4th of the histogram
i_34 = 3 * (n_points // 4)      # 3/4th of the histogram
corner_labels = (list(range(i_14 - w, i_14 + w + 1)) +
                 list(range(i_34 - w, i_34 + w + 1)))
label_sets = (edge_labels, flat_labels, corner_labels)

for ax, labels in zip(ax_img, label_sets):
    ax.imshow(overlay_labels(image, lbp, labels))

for ax, labels, name in zip(ax_hist, label_sets, titles):
    counts, _, bars = hist(ax, lbp)
    highlight_bars(bars, labels)
    ax.set_ylim(top=np.max(counts[:-1]))
    ax.set_xlim(right=n_points + 2)
    ax.set_title(name)

ax_hist[0].set_ylabel('Percentage')
for ax in ax_img:
    ax.axis('off')

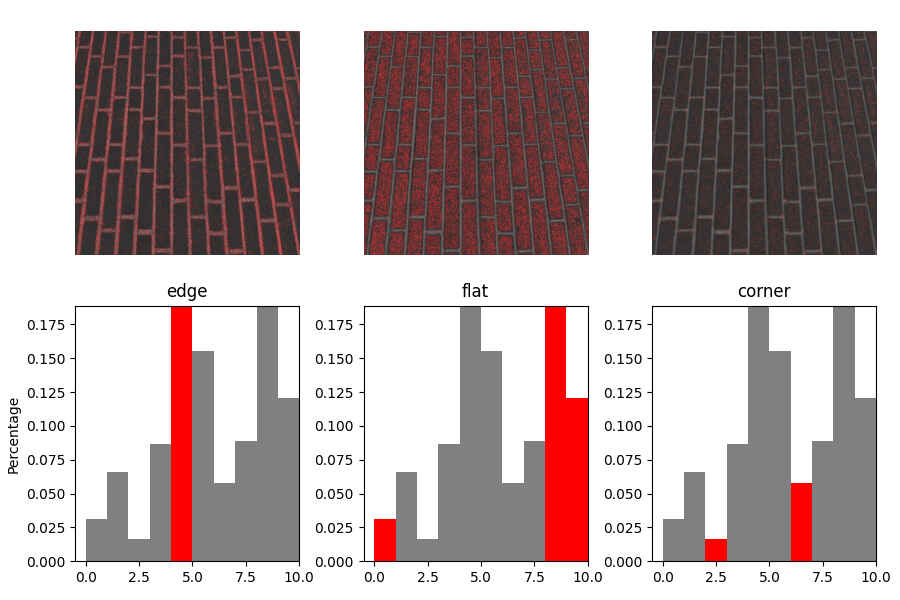
上面的代码中，因为参数radius=1, num_points=8，mode=uniform，因此其对应的二进制LBP编码有9种，其中00000000和11111111表示平坦的面，00001111表示边，00111111和00000011表示角，如上图所示。

当然，上面是以最简单的radius=1介绍的，当使用更大的半径取更多的点时，每个点上的像素值是通过双线性插值来计算的。LBP算法还有很多变体和改进，如旋转不变LBP、对称LBP、多尺度LBP等，需要根据具体应用场景和需求选择合适的算法和参数。

(adsbygoogle = window.adsbygoogle || []).push({});

# 参考资料

← Haar特征 →