天天教程

# 双边滤波BilateralFilters

# 1.高斯滤波

# 1.1 理论

高斯滤波器是一种线性滤波器，能够有效的抑制噪声，平滑图像。其作用原理和均值滤波器类似，都是取滤波器窗口内的像素的均值作为输出。其窗口模板的系数和均值滤波器不同，均值滤波器的模板系数都是相同的为1；而高斯滤波器的模板系数，则随着距离模板中心的增大而系数减小。所以，高斯滤波器相比于均值滤波器对图像个模糊程度较小。

二维高斯函数表达式：

h(x,y)=Ke−x2+y22σ2

卷积核大小,表示的是距离卷积核中心的距离

r=(x−k/2)2+(y−k/2)2h(r)=Ke−r22σ2

其中类似于正态分布的方差，控制着高斯函数的型态。

越大，分布越分散，各部分比重差别不大，于是生成的模板各元素值差别不大，类似于平均模板；

越小，分布越集中，中间部分所占比重远远高于其他部分，反映到高斯模板上就是中心元素值远远大于其他元素值，于是自然而然就相当于中间值的点运算。

取,则高斯函数为，

h(r)=1sπσe−r22σ2

对于卷积核大小为的高斯核为：

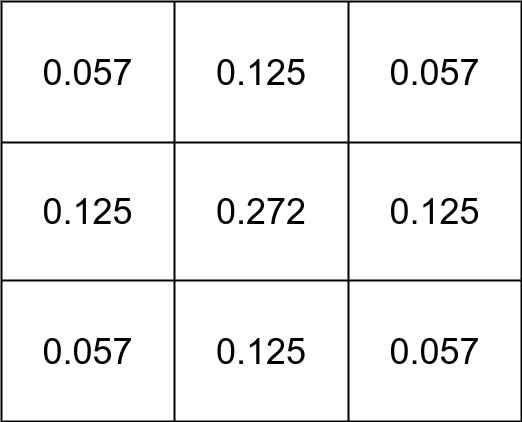
高斯核主要用来对图像做平滑。

# 1.2 示例

OpenCV中有GaussianBlur的API函数，调用时只需给出kernel size和sigma即可。

cv::Mat dst;
cv::GaussianBlur(img, dst, cv::Size(7, 7), 0.9);
cv::imshow("Before Gaussian Blur", img);
cv::imshow("After Gaussian Blur", dst);
cv::waitKey(0);

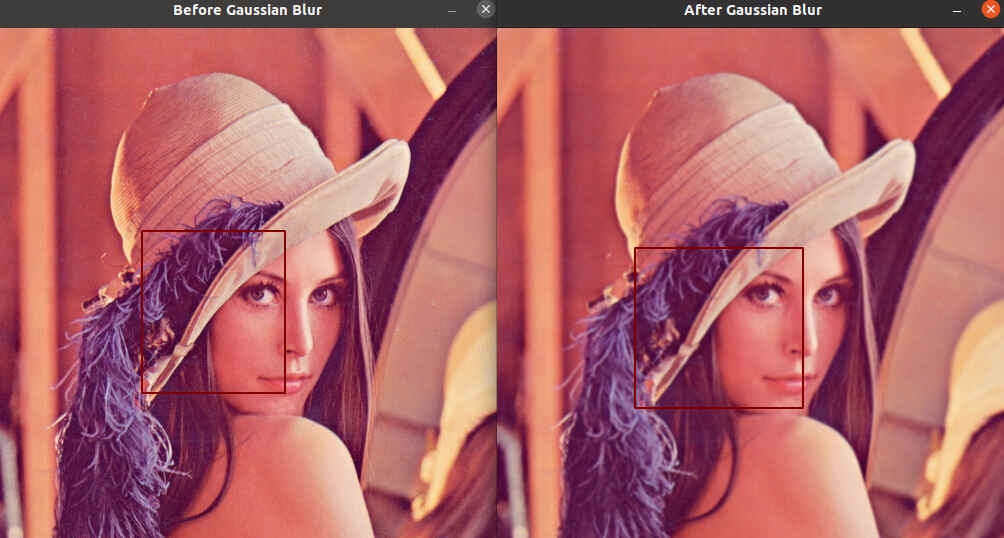
上图中，可以看到平滑后红框中的帽子边沿变模糊了。

# 2.双边滤波（Bilateral Filter）

# 2.1 理论基础

第一部分介绍的高斯滤波在对图像进行平滑操时，对所有的像素都是无差别的使用同个高斯核进行计算的，这会导致对图像中物体边缘也进行平滑，使图像变的模糊。

为了解决高斯滤波会导致边缘模糊的问题，不仅需要考虑像素之间的空间关系，还需要考虑卷积核范围内的像素值间的变化大小。对像素值变化大的位置，考虑有可能是边缘，增大该位置的权重。

回顾一下，高斯模糊的公式为：

其中表示的是像素位置处Gaussian Blur后的结果，表示的高斯核，表示的是高斯核所覆盖的函数，表示的是高斯函数，表示的是位置处的像素值。

双边滤波算法Bilateral Filter不仅考虑了位置，还考虑了像素值的变化，因此双边滤波的公式为：

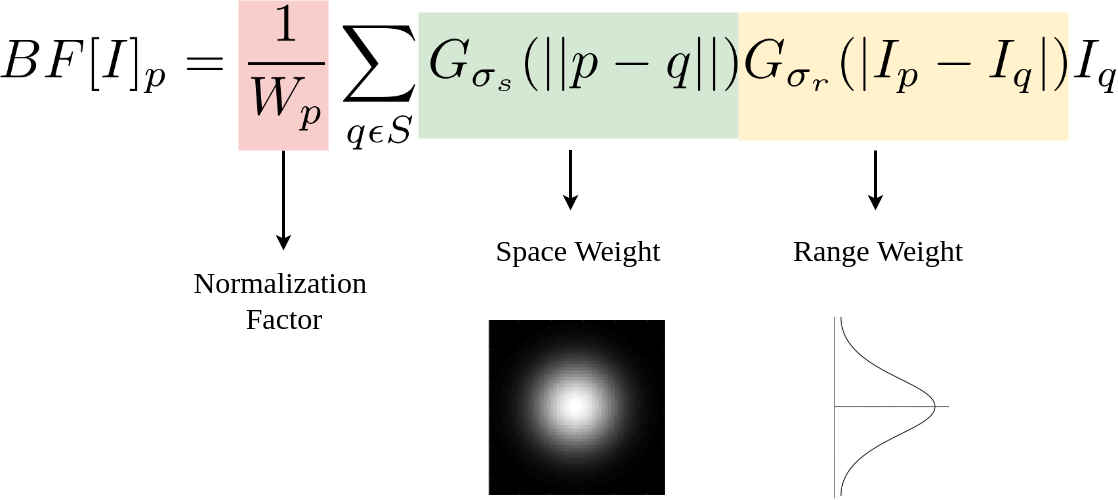
其中表示的是像素位置处Bilateral Filter后的结果，是定义在像素差值上的高斯函数。

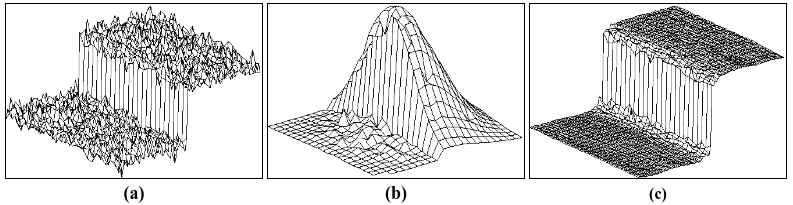
上面这幅图中，表示的是一幅有边缘的图像像素值变化，图表示的是一个23x23的双边滤波的核，图表示的是对使用双边滤波后得到的结果，可以看到有效的对图像进行了平滑，并保留了边缘信息。

# 2.2 OpenCV bilateralFilter函数

cv::Mat dstb, dstg;
cv::GaussianBlur(img, dstg, cv::Size(3,3), 0.8);
cv::bilateralFilter(img, dstb, -1, 75, 0.8);
cv::imshow("Origin", img);
cv::imshow("After Gaussian Blur", dstg);
cv::imshow("After Bilateral Filter", dstb);
cv::waitKey(0);

效果对比如下：

点开图像看原图，在图中红色框出的部分，能够看到双边滤波在平滑的同时还有非常好的保边能力。

(adsbygoogle = window.adsbygoogle || []).push({});

# 参考资料

单应矩阵 →