天天教程

# CTC算法

# 1.基础介绍

论文：Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks (opens new window)

这是2006年第23次ICML会以上的一篇论文。

很多实际应用需要从未切分的数据中输出序列信息，如语音识别中的语音转文字,光学字符识别(Optical character recognition,OCR)中的字符图片转字符序列。循环神经网络(Recurrent neural networks,RNN)十分适合序列数据的学习，但其训练数据要求必须是切分后的序列，而实际应用中切分的训练序列数据标注比较困难，是很难获取的。

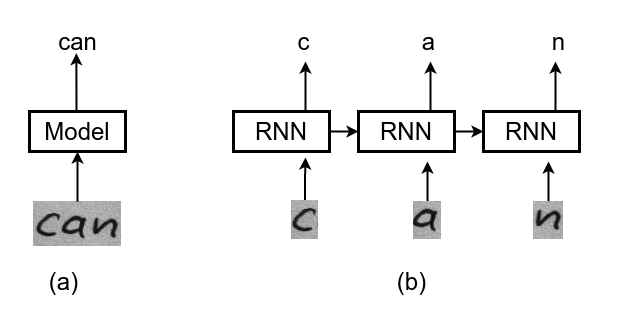
上图是OCR的两种模型，一种如图(a)可直接输入OCR检测得到的图片得到图片中的字符串can，另外一种需要先将图片按字符进行切割，这种方式比较数据处理比较复杂，而这种正是循环神经网络RNN要求的输入。

为了充分利用循环神经网络RNN处理序列数据的能力，同时避免对输入序列图像进行切分，本文作者提出了Connectionist Temporal Classificatio(CTC)算法。

# 2.Connectionist Temporal Classification(CTC)算法

# 2.1 什么是Temporal Classification

是从分布从获取的训练数据，
输入空间是维的实值向量序列，目标空间由字母集组成的标签序列，训练数据集中的每个样本由序列对组成。目标序列长度小于等于输入序列。输入序列和输出序列长度一般不同，因此没有先验知识可以对齐他们。

Temporal Classification的任务是使用训练数据,学习一个分类器，能够将输入序列分成对应的目标序列

从第一部分介绍，可以知道OCR任务本身就是一个Temporal Classification，翻译成了时间序列分类问题。其输入是卷积后得到特征图序列，输出的是字符序列。

之所以被称为Connectionist Temporal Classification，是这样理解的，原始输入的是一整张联结在一起未切分的字符图像，输出的是字符序列，因为没有对原始图像上的字符进行切分预处理，因此被称之为连接序列分类。

# 2.2 CTC问题描述

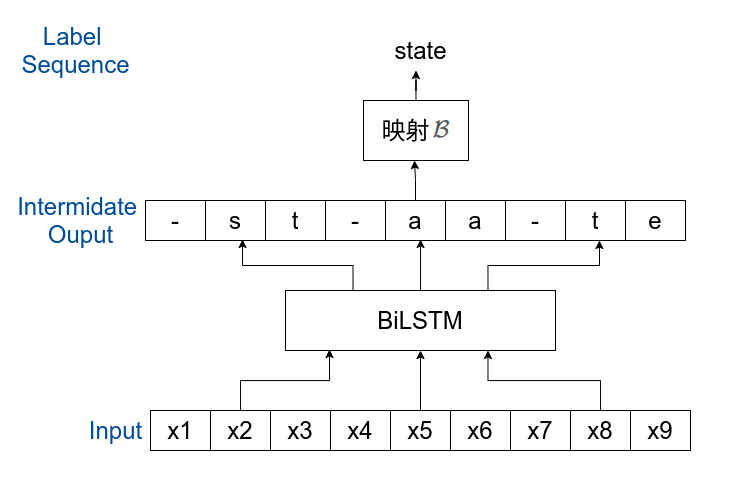
从网络输入到获取标签序列要分成两步：

第一步，可以将输入为长度为的序列(序列中每个都是m维),输出为长度的序列(序列中每个都是n维),参数为的映射(即循环神经网络)定以为，。将表示成第个序列值为的概率，L'^T表示长度为的序列,其中每个元素取自字母集，序列L'^T也被称之为路径，表示成。

根据以上定义给定输入,输出为路径的概率可表示成：

p(π|x)=∏t=1Tyπtt,∀π∈L′T

其实，这里还有个条件，就是每一步输出之间是相互独立，上面的公式才能成立。

第二步，我们知道输入对应的标签序列为长度等于的序列，,在第一步中循环神经网络给出的只是长度为的中间序列,要和长度为的标签序列对应，还需要定义个从中间序列到标签序列的映射\mathcal{B}:L'^T\mapsto L^{\lt T},很明显，是一个多对一的映射。这个映射可以定义为移除中间序列中的重复相邻字符和空格占位符，如,定义了映射后，可以将输出标签序列的后验概率表示成：

p(z|x)=∑π∈B−1(z)p(π|x)

# 2.2关于对齐

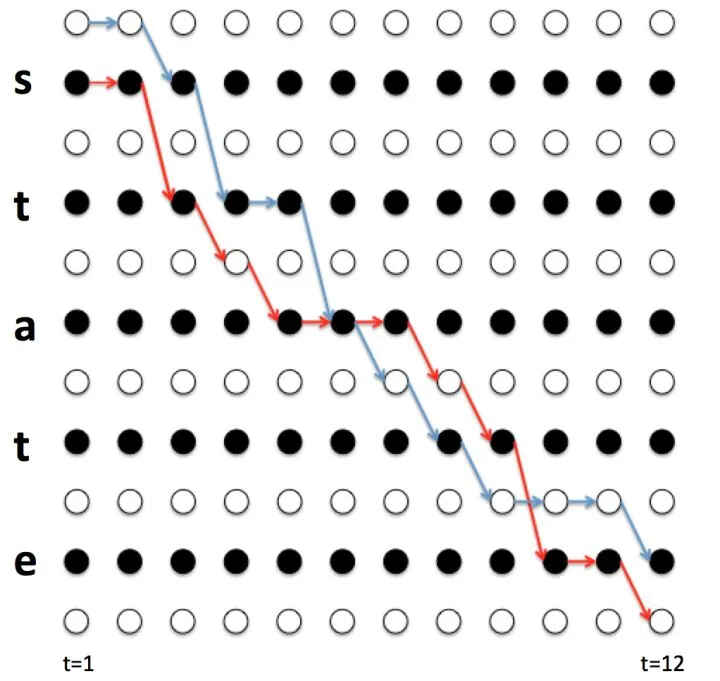
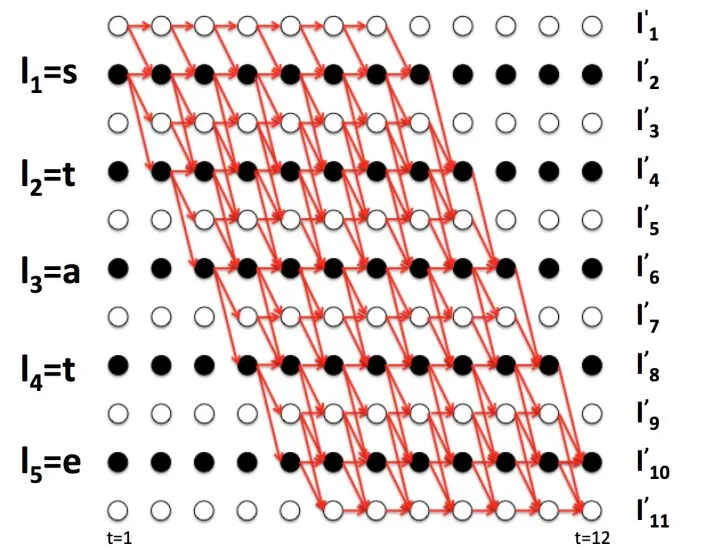
为什么要使用上述的方法来进行网络的训练呢？那是因为输入和标签序列之间在序列长度，序列长度比例，对应元素之间找不到什么对应关系。

(opens new window)

如上图是对齐后的数据，但在实际中是很难知道,标注这样的数据也需要花费大量的时间，因此更希望模型能够拥有从未对齐数据中学习的能力，通过前面的介绍，使用CTC算法可以从未对齐的输入中求得标签序列。

# 2.3 前向后向算法

使用暴力方法计算

p(z|x)=∑π∈B−1(z)p(π|x)

因为要计算每一条路径，因此对于序列字典中有个元素，长度为的序列，要计算所有路径的概率，时间复杂度为，这是指数级的时间复杂度，对于大部分长度的序列这个运算都过于耗时。论文作者为了解决这个问题，提出了前向后向递推算法，采用动态规划的方法将时间复杂度降到了,使算法更可行。

先借个例子来看一下。

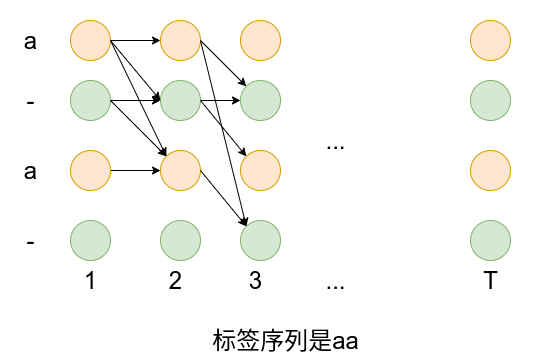
假设标签序列为

z=state

在序列前后和每个字符中间添加空格占位符：

z′=−s−t−a−t−e−

对中任意的字符重复任意次，经过映射都能得到标签序列，因此可以将当成满足变换条件的基础序列。是多对一的映射，如下4个路径都能得到

B(−−sttaa−tee−)=stateB(−−stta−t−−−e)=stateB(sst−aaa−tee−)=stateB(sst−aa−t−−−e)=state

将写成列的形式，则上述四条路径可以写成如下图的形式：

(opens new window)

从上图可以看到，四条路径在序列时都经过字符,记上面的四条路径为

π1=b=b1:5+{a}6+b7:12π2=r=r1:5+{a}6+r7:12π3=b1:5+{a}6+r7:12π4=r1:5+{a}6+b7:12

记表示序列第步元素为的概率，则上面四条路径都包含这一项，将计算上面四条路径的概率表示可以提取公因式写成：

foward=p(b1:5+r1:5|x)=y−1∗y−2∗ys3∗yt4∗yt5+ys1∗ys2∗yt3∗y−4∗ya5backward=p(b7:12+r7:12|x)=y−7∗yt8∗y−9∗y−10∗y−11∗ye12+ya7∗y−8∗yt9∗ye10∗ye11∗y−12

然后上面四条路径的概率和可以写成：

p(π1,π2,π3,π4|x)=forward∗ya6∗backward

上面的介绍中只取了四条经过变换后能得到的路径，实际上的路径要远远多于此：

(opens new window)

从上图中选出经过的所有路径，概率(表示路径的第6个字符为a),同样还是可以表示成如下形式:

进一步推广，定义表示路径中的第t个字符与加了占位符后标签序列的第s个字相对应且路径满足时所有路径的概率和,表示成：

αt(s)=∑B(π1:t)=留−z1:s′∏t′=1tyπt′t′

可以看到这等同于前向变量，现在来看时的,要经过映射后能得到保留占位符的标签序列，就只能等于1或者2，看上图中的例子，t=1时刻只能取的或者,否则无法经过映射得到标签序列，因此

α1(1)=y−1α1(2)=yz2′1α1(s)=0,∀s>2

还看的例子，当过时，对应的字符只能是,可以推出来上面例子中

α6(6)=(α5(4)+α5(5)+α5(6))∗ya6

一般化推广可得：

αt(s)=(αt−1(s−2)+αt−1(s−1)+αt−1(s))∗yzs′t

还需考虑一个特殊情况，看下面例子,t=2,s=6或3:

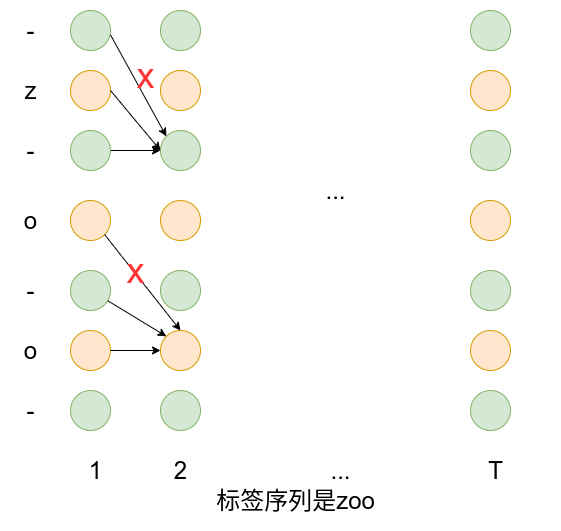
很明显因为映射会去除重复的字母，因此上面两种情况在时刻不能取

综上，可得最终时前向递推公式为(也就是原论文上的递推公式)：

αt(s)={(αt−1(s−1)+αt−1(s))∗yzs′tifzs′=−orzs′=zs−2′(αt−1(s−2)+αt−1(s−1)+αt−1(s))∗yzs′totherwise

将公式中相同的项合并一下就可以得到论文上的公式了。

同样的方法可以定义:

βt(s)=∑B(πt:T)=留−zs:|z′|′∏t′=tTyπt′t′

时的递推公式：

βt(s)={(βt+1(s)+βt+1(s+1))∗yzs′tifzs′=−orzs′=zs+2′(βt+1(s)+βt+1(s+1)+βt+1(s+2))∗yzs′totherwise

求得和后，标签序列的后验概率可以写成，

p(z|x)=∑zs′∈πtαt(s)βt(s)yzs′t

求得后，可以知道使用时的目标就是最大化,可以定义损失函数为，可以推导损失的计算和损失函数梯度都能使用递推的方式来计算，减少运算量，加快运算速度。

# 2.4 推理时

训练完成后，在网络推理时希望取概率最大的输出序列：

z∗=argmaxzp(z|x)

对所有路径的概率求和，然后取概率最大的路径作为预测的结果，应该是最合理的方式，但当序列比较长时面临计算量过大，影响推理速度的情况。

一种做法是对于第步，取概率最大的字符，然后将所有的字符组合起来经过去重当作最终的输出，但这种做法只考虑了一条路径，有可能有多条路径对应标签，各条路径的概率加和后有可能更大。

一种替代的折衷方法是改进版的Beam Search。

常规的Beam Search算法，对于每个时间步取概率最大的几个(Beam Size)可能结果，如下为字母集为，Beam Size=3的Beam Search的过程：

(opens new window)

上图中Beam Search到当前步最大的几个(Beam Size)可能字符都只有一条前缀序列，实际上可以有多条前缀序列和当前的字符组合后都得到相同的输出，如下图对于路径长度时,,最后都能对应的

a a a b a a a b b a ϵ a b ϵ a b ϵ a b λ a b ϵ a b ϵ a b ϵ a b λ ϵ a b T = 4 T = 3 T = 2 T = 1 current hypotheses proposed extensions current hypotheses proposed extensions current hypotheses proposed extensions current hypotheses Multiple extensions merge to the same prefix empty string

且观察时，前缀序列对应的输出有可能是或者,因此对应的概率应该分别进行计算。

# 3.pytorch中的CTCLOSS

计算未切分的连续时间序列和目标序列之间的损失。 (opens new window)

torch.nn.CTCLoss(blank=0, reduction='mean', zero_infinity=False)

class CTCLoss:
     ...
     def forward(self, log_probs: Tensor, targets: Tensor, input_lengths: Tensor, target_lengths: Tensor) -> Tensor:
          ...

  • log_probs：Tensor of size (T,N,C)/(T,C),T是输入长度，N是Batch Size，C是序列字典的大小(包括空格)

  • targets：Tensor of size（N，S）N是batch size，S是最大目标序列长度，目标序列中的每个元素是类别的序号。

  • input_lengths，每个输入序列的长度，为元组tuple或shape为(N,)的张量，N是batch size，input_lengths的值

  • target_lengths,每个目标序列的长度，为元组tuple或shape为(N,)的张量，N是batch size，如果targets的shape是(N,S),这里其实是把每个添加padding后变成了S，假设第n个序列目标长度为,target_lengths中第n个元素值就为。

import torch

T = 2
C = 3
N = 1
S = 2
S_min = 1

input = torch.randn(T,N,C).log_softmax(2).detach().requires_grad_()
print(input)
target = torch.tensor([0,1], dtype=torch.long).reshape(shape=(N, S))
print(target)
input_lengths = torch.full(size=(N,), fill_value=T, dtype=torch.long)
target_lengths = torch.tensor([2], dtype=torch.long).reshape(shape=(N,)) 
ctc_loss = torch.nn.CTCLoss()
loss = ctc_loss(input, target, input_lengths, target_lengths)
print(loss)

# tensor([[[-0.4002, -1.5314, -2.1752]],         [[-0.8444, -2.2039, -0.7770]]], requires_grad=True)
# tensor([[0, 1]])
# tensor(1.3021, grad_fn=<MeanBackward0>)

上面示例的计算过程：


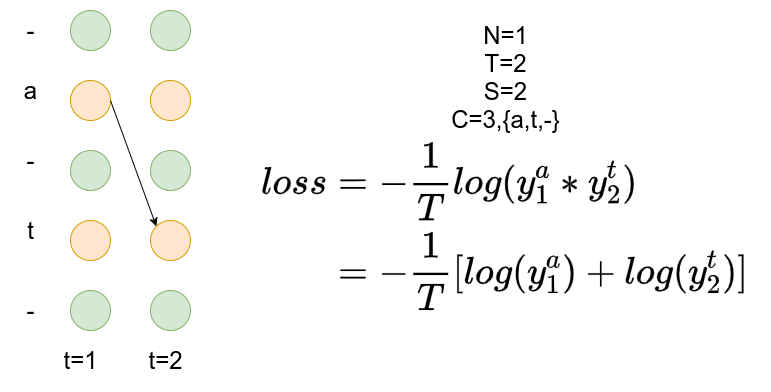
从上图可以看到目标是即at路径有且仅有此一条，损失值计算为：

loss=−12[−0.4002+(−2.2039)]=1.3021
(adsbygoogle = window.adsbygoogle || []).push({});

# 参考资料

←