天天教程

# 编辑距离

72. 编辑距离 (opens new window)

# 问题

给两个单词 s1 和 s2， 返回将 s1 转换成 s2 所使用的最少操作数  。

你可以对一个单词进行如下三种操作：

  • 插入一个字符
  • 删除一个字符
  • 替换一个字符
输入：s1 = "horse", s2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/edit-distance
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

# 解法

# 自顶向下

如上图演示了s1从rad通过最少次编辑变成apple(s2)的过程。

这里是从顶向下的一种思想，非常直观。

观察图很容易发现，在s1的位置i处根据不同状态对应的可选动作总共有四种：

  • 状态1:s1位置i处的字符与s2位置j处的字符不相同
    • 1）删除i位置的字符，i后移一位。
    • 2）往s1中增加一个字符，j后移一位。
    • 3）替换操作，将s1位置i处的字符替换成s2位置j处的字符，i和j同时后移一位。
  • 状态2:s1位置i处的字符与s2位置j处的字符相同
    • 1）直接跳过，i和j同时后移一位。

状态1中有3种动作可以选，如何确定应该选哪个动作呢？

很自然的一个想法是采用哪个动作后接下来需要的编辑距离最小，就采用哪个动作。写成伪代码：

int dp(string s1, int i, string s2, int j) {
    ...
    if(s1[i]!=s2[j]) {
        int del_n = dp(s1, i-1, s2, j);
        int add_n = dp(s1, i, s2, j-1);
        int rep_n = dp(s1, i-1, s2, j-1);
        return min(del_n, add_n, rep_n);
    }
}

通过上面的理解，很容易写出递归形式的解答代码，需要给上面的伪代码加入终止条件，也就是当s1为空或s2为空时的处理。添加终止条件后，还需要处理s1[i]==s2[j]的状态，最后，代码如下：

int dp(string s1, int i, string s2, int j) {
    if(i < 0) return j + 1;
    if(j < 0) return i + 1;
    if(s1[i]==s2[j]) {
        return dp(s1, i-1, s2, j-1);
    }
    if(s1[i]!=s2[j]) {
        int del_n = dp(s1, i-1, s2, j);
        int add_n = dp(s1, i, s2, j-1);
        int rep_n = dp(s1, i-1, s2, j-1);
        return min(del_n, add_n, rep_n);
    }
}

上面的自顶至底的状态转移过程，从dp[i][j]到dp[i-1][j-1]的路径有多条，如dp[i][j]->dp[i-1][j-1]和dp[i][j]->dp[i-1][j]->dp[i-1][j-1]，因此存在重复路径，也就意味着有大量的重复运算。

可以使用备忘录优化递归代码，或者将代码写成动态规划的形式。

# 自底向上

将horse变成ros的过程，

上述表示的是dp表格的初始状态，该dp表格表示的是s1到第i位置的子串变换成s2到第j位置的子串所需要的最小编辑距离。

上图初始状态表示的含义，

  • s1=''时变成s2需要的动作就是插入，如表中从左到右的一行表示往s1中插入字符变成s2
  • s2=''时，将s1变成s2所需要的操作就是把s2中的每个字符都删除，如表中从上到下的一列表示删除s1中的字符的操作。

总结，在dp表格中，

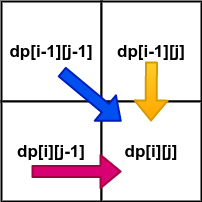
  • 从左向右表示往s1中插入当前字符，如下图中红色箭头所示意；
  • 从上到小表示从s1中删除
    字符，如图中黄色箭头所示；
  • 斜对角表示的是替换操作，如图中蓝色箭头所示。

写成代码形式为：

int minDistance(String s1, String s2) {
    int m = s1.length(), n = s2.length();
    int[][] dp = new int[m + 1][n + 1];
    // base case 
    for (int i = 1; i <= m; i++)
        dp[i][0] = i;
    for (int j = 1; j <= n; j++)
        dp[0][j] = j;
    // 自底向上求解
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (s1.charAt(i-1) == s2.charAt(j-1)) {
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                dp[i][j] = min(
                    dp[i - 1][j] + 1,
                    dp[i][j - 1] + 1,
                    dp[i - 1][j - 1] + 1
                );
            }
        }
    }
    return dp[m][n];
}

# reference