天天教程

# Weisfeiler Lehman算法

Weisfeiler-Lehman Algorithm是美国的数学家Boris Weisfeiler (opens new window)在1968年发表的论文the reduction of a graph to a canonical form and an algebra arising during this reduction (opens new window)中提出的判断图同构(Graph Isomorphism)与否的算法。

# 1.图同构介绍

参考自维基百科 (opens new window)

图同构描述的是图论中，两个图之间的完全等价关系。在图论的观点下，两个同构的图被当作同一个图来研究。

只有节点数目相同(即同阶)的两个图才有可能同构。

两个简单图和称为是同构的，当且仅当存在一个将的节点映射到的节点的一一对应 ，使得中任意两个节点和相连接，当且仅当中对应的两个节点和相连接。同构可记作。

一组彼此同构的图可称为同构图。

一幅图经常可以有多种不同的方式在纸上或屏幕上画出来，所以两个看起来很不同的图也可能是同构的。尤其当图的节点数比较大时，很难一眼从画出的图上判断它们是否同构。

# 2.Weisfeiler-Lehman Algorithm

第一部分介绍了什么是图同构，Weisfeiler-Lehman算法正是为了用来判断图是否同构的算法，因此也被称为Weisfeiler-Lehman Isomorphism Test,不过现在已经发现，单纯的通过该算法还不能够确保图同构。

图中的节点表示为,边表示为,节点的集合表示为，边的集合表示为，如此图可以表示为。

Weisfeiler-Lehman算法是通过进行多次迭代，然后判断节点上的标签值的个数是否一致来判断图是否同构。

算法中：

  • 表示算法迭代的次数
  • 表示第个节点
  • 表示节点邻居节点标签的集合(multiset,A multiset is a set where elements may appear multiple times.)
  • 表示算法每一次迭代中给每个节点赋予的标签值。相同的节点也相同。

算法步骤：

  • 1)开始时初始化所有节点
  • 2)第步，对于每个节点,定义是由i-1步的C_{i-1,m}组成的m是节点n$的所有邻居节点。
  • 3)计算
  • 4)统计每种标签值节点的个数，重复步骤2)和3)N步或算法收敛。

例如：

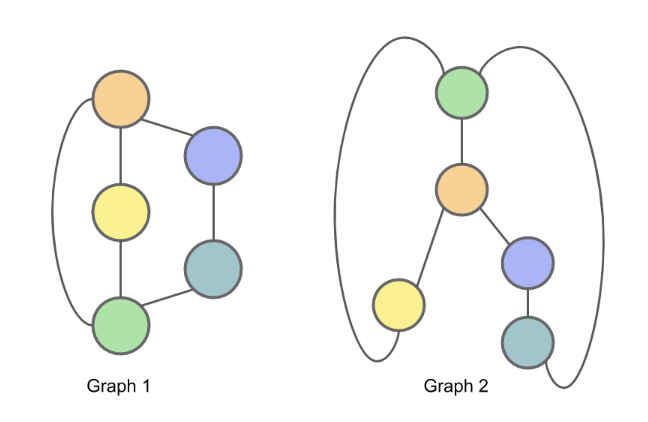
下图中Graph1和Graph2是同构的：

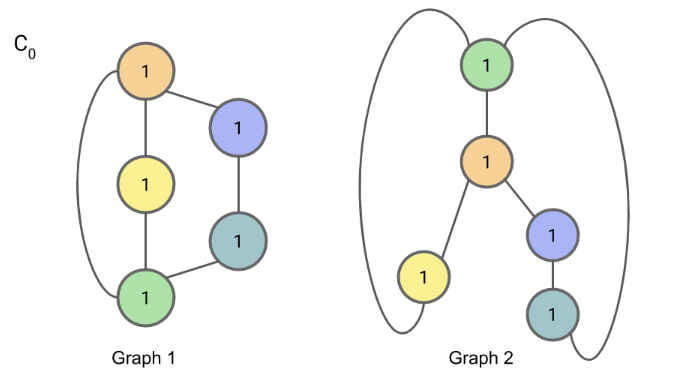
初始化：

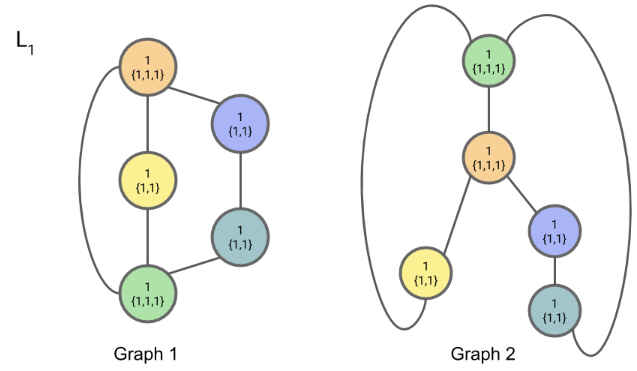
对于iteration=1


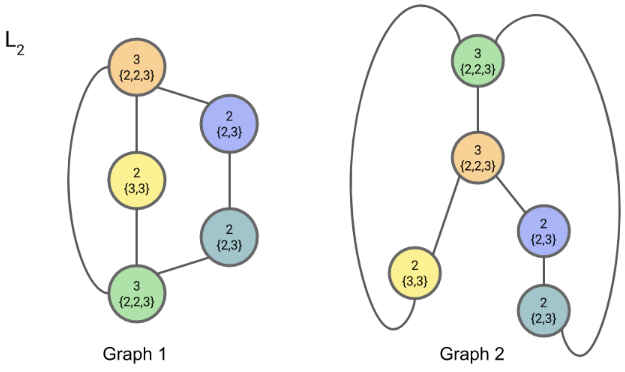
对于iteration=2


对于iteration=3


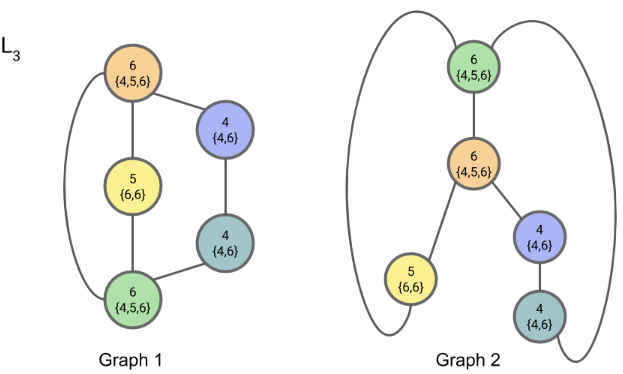
到第3步可以看到两个图中都是有2个7，1个8，2个9， 因此，两个图是同构的。

# 3.后话

关于算法作者Boris Weisfeiler (opens new window),是一个数学家，其本身是犹太人，出生在苏联，后转到美国，但是在1985年于智利神秘失踪，生死未卜。

(adsbygoogle = window.adsbygoogle || []).push({});

# 参考资料