线性代数的常用操作

1.向量的内积

• 定义
  
  向量的内积即点乘，其定义如下：
  
  向量
  向量
  
  和的内积公式表示为：
  
  
• 几何意义
  
  两个向量之间的夹角，向量在向量上的投影。

2.向量的外积

• 定义

$$\overrightarrow{a}\times \overrightarrow{b}=\left[\begin{array}{ccc}\overrightarrow{i}& \overrightarrow{j}& \overrightarrow{k}\\ a_1& b_1& c_1\\ a_2& b_2& c_2\end{array}\right]=\left[\begin{array}{c}{b}_1{c}_2-b_2{c}_1\\ a_2{c}_1-a_1{c}_2\\ a_1{b}_2-a_2{b}_1\end{array}\right]=\left[\begin{array}{ccc}0& -c_1& b_1\\ c_1& 0& -a_1\\ -b_1& a_1& 0\end{array}\right]\overrightarrow{b}={\overrightarrow{a}}^{\wedge }\overrightarrow{b}$$

式中符号表示把向量写成一个反对称矩阵。

即：

$${\overrightarrow{a}}^{\wedge }=\left[\begin{array}{ccc}0& -c_1& b_1\\ c_1& 0& -a_1\\ -b_1& a_1& 0\end{array}\right]$$

• 几何意义

外积的结果是一个向量，该向量的模等于向量和向量围成的平行四边形的面积

3.正交向量

向量的内积等于两个向量长度乘上向量之间的夹角，当两个向量之间夹角的余弦值等于0时，在二维空间，我们称之为垂直，在高维空间中我们称之为正交。

因此正交向量是内积为零的向量。

4.正交向量组

正交向量组是指一组两两正交且非零的向量。

如果维的向量组：两两正交，那么，它们彼此之间一定线性无关。即不存在一组不为0系数满足：

$${\lambda }_1\overrightarrow{a_1}+{\lambda }_2\overrightarrow{a_2}+...+{\lambda }_r\overrightarrow{a_r}=0$$

证明很简单，只需要左右同时乘以一个,发现只有时上式才成立。

5.向量空间的基与维数

向量空间的定义，向量空间由所有的n维向量组成，向量中的每个元素都是实数。

设为向量空间，如果个向量，且满足：

• 线性无关;
• 中任一向量都可由线性表示，也就是可由它们生成整个空间。

那么，向量组就称为向量空间的一组基，称为向量空间的维数。

对于给定向量空间，虽然会有很多组基，但空间中的任一组基都有相同的向量的数量。

基向量可能不同，但基向量的个数一定相同。

把正交向量组的概念和基的概念融合，设向量组是向量空间的一个基，若它们之间彼此正交，那么就称它们是一组规范正交基。

对于一个向量，可以很方便地求出它在规范正交基下各个维度的坐标：

$${\lambda }_i={\overrightarrow{a_i}}^T\overrightarrow{a}$$

即对于向量，在规范正交基下某一个维度的坐标，等于它和整个维度的正交基向量的内积。

若已知向量空间中的一组基，如何求的规范正交基呢？

可以使用施密特算法对基进行规范正交化，该算法公式可写成：

$$\begin{array}{rl}{b}_1& =a_1\\ b_2& =a_2-\frac{[b_1,a_2]}{[b_1,b_1]}{b}_1\\ ...\\ b_r& =a_r-\frac{[b_1,a_2]}{[b_1,b_1]}{b}_1-\frac{[b_2,a_2]}{[b_2,b_2]}{b}_2-...-\frac{[b_{r-1},a_{r-1}]}{[b_{r-1},b_{r-1}]}{b}_{r-1}\end{array}$$

上式中表示两个向量的内积。

将单位归一化后即可求得规范正交基。

6.正交矩阵

正交矩阵矩阵是转置等于逆的方阵，即满足

$$A^{T}A=E$$

三个性质，

• ,且都是正交矩阵，
• A和B都是正交矩阵，并且它们阶数一样，那么AB也是正交矩阵
• A是正交矩阵，向量y经过A变换之后行列式保持不变

7.反对称矩阵

反对称矩阵是一个方阵，其转置矩阵和自身的加法逆元相等，即

8.齐次坐标与齐次变换矩阵

简而言之，齐次坐标就是用N+1维来代表N维坐标。最后新增的一维值为1或0(无穷远处的点)。
齐次(homogeneous)从字面上解释是“次数相等”的意思。使用齐次坐标的方便之处在于，对笛卡尔点齐次坐标的任何标量的乘积仍然表示同一个笛卡尔点。齐次坐标有规模不变性。因此被称为齐次坐标。如齐次坐标都表示同一个笛卡尔点。对齐次坐标进行变换的矩阵称为齐次变换矩阵。

9.相似矩阵

A和B都是n×n的方阵，若存在可逆矩阵M，使得，则称A和B互为相似矩阵，记作A~B。相似矩阵具有同样的特征值。

如果A有n个线性无关的特征向量，则A可以对角化为，相当于，A和其特征值矩阵Λ互为相似矩阵，这里的M=S，是特征向量矩阵。实际上A的相似矩阵有很多，我们可以用任意可逆矩阵M代替S，从而求得其他的相似矩阵，Λ是众多相似矩阵中最简洁的一个。

对于,设A，B和C是任意同阶方阵，则有：

（1）反身性：A~A

（2）对称性：若A~B，则B~A

（3）传递性：若A~B，B~C，则A~C

（4）若A~B，则二者的特征值相同、行列式相同、秩相同、迹相同。

（5）若A~B，且A可逆，则B也可逆，。

10.相似对角化

如果一个方阵相似于对角矩阵，也就是说存在一个可逆矩阵使得是对角矩阵，则就被称为可以相似对角化的。

矩阵

$$A=\left[\begin{array}{cc}1& -2\\ -2& 1\end{array}\right]$$

的相似对角化为

$${\left[\begin{array}{cc}-1& 1\\ -1& -1\end{array}\right]}^{-1}\left[\begin{array}{cc}1& -2\\ -2& 1\end{array}\right]\left[\begin{array}{cc}-1& 1\\ -1& -1\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& 3\end{array}\right]$$

使用numpy计算的特征值和特征向量可知：

from numpy import linalg as LA
import numpy as np
mat = np.array([[1, -2],[-2, 1]])
W, V = LA.eig(mat)
print(W,V)
"""output
[ 3. -1.] 

[[ 0.70710678  0.70710678]
 [-0.70710678  0.70710678]]
"""

对角矩阵中的元素是的特征值。

相似对角化的好处：

• 1）相似对角化使得同一个线性变换表达方式变的简单

图片引用自https://zhuanlan.zhihu.com/p/138285148 (opens new window)

• 2）通过相似对角化（实际为坐标轴旋转）可以消去二次型中的交叉项

图片引用自https://zhuanlan.zhihu.com/p/138285148 (opens new window)

11.方阵的特征分解

对于的矩阵的特征值分解为,的每一列都是特征向量，对角线上的元素是从大到小排列的特征值。

当矩阵是一个对称矩阵时，则存在一个对称对角化分解，即,的每一列都是相互正交的特征向量，且是单位向量，对角线上的元素是从大到小排列的特征值。将矩阵记作,则矩阵A可以写为：

$$A={\lambda }_1{\overrightarrow{q}}_1{\overrightarrow{q}}_1^T+{\lambda }_2{\overrightarrow{q}}_2{\overrightarrow{q}}_2^T+...+{\lambda }_m{\overrightarrow{q}}_m{\overrightarrow{q}}_m^T$$

12.矩阵的奇异值分解SVD

当给定一个大小为的矩阵A，虽然矩阵A不一定是方阵，但大小为的和的却是对称矩阵，若，，则矩阵A的奇异值分解为:

$$A=P\mathrm{\Sigma }{Q}^T$$

P的列向量称为矩阵A的左奇异向量，Q中的列向量称为矩阵A的右奇异向量，矩阵大小为,矩阵大小为,两个矩阵对角线上的非零元素相同，矩阵的大小为,位于对角线上的元素称为奇异值。若矩阵对角线的非零元素为,这些特征值也都是非负的，且与对角线上的非零元素相同，则矩阵对角线上的元素为：

$${\sigma }_1=\sqrt{{\lambda }_1},{\sigma }_2=\sqrt{{\lambda }_2},...,{\sigma }_k=\sqrt{{\lambda }_k},$$

U\V分别有什么几何意义呢？后面再补充。
奇异值分解的几何含义为：对于任何的一个矩阵，我们要找到一组两两正交单位向量序列，使得矩阵作用在此向量序列上后得到新的向量序列保持两两正交。

考虑方阵可以进行特征值分解，常规矩阵就无法进行特征分解，就是奇异值分解，称为主特征值分解更好理解。就可以类比于特征矩阵的逆和特征矩阵。

在奇异值分解中，较大的奇异值会决定原矩阵的“主要特征”，可以使用奇异值分解的低秩逼近来截取原矩阵中的主要成分 (opens new window)。numpy.linalg中提供了函数可用来计算矩阵的奇异值分解：

from numpy import linalg as LA
import numpy as np
mat = np.array([[4, 4],[-3, 3]])
u,s,v = LA.svd(mat)
print(u)
print(s)
print(v)
"""output
[[-1.00000000e+00  0.00000000e+00]
 [ 3.70074342e-18  1.00000000e+00]]

[5.65685425 4.24264069]

[[-0.70710678 -0.70710678]
 [-0.70710678  0.70710678]]
"""

12.1 SVD求齐次矩阵方程的最小二乘解

这里用到了几个性质，

一个是向量的二范数的定义，以
\vec{v}=\begin{bmatrix}x_1\\x_2\end{bmatrix}为例，

是正交矩阵，因此,

$$||U^T\overrightarrow{v}|{|}_2=\sqrt{{\overrightarrow{v}}^{T}U{U}^T\overrightarrow{v}}=\sqrt{{\overrightarrow{v}}^T\overrightarrow{v}}$$

因此乘以并不改变二范数。

求解超定方程，相当于在两侧乘以,然后再代入的SVD分解来求解最小二乘解。

更进一步，根据SVD定义的伪逆的概念可以直接求解最小二乘解。

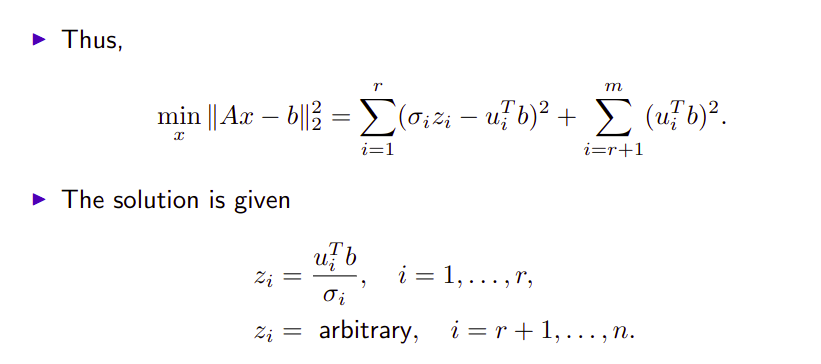
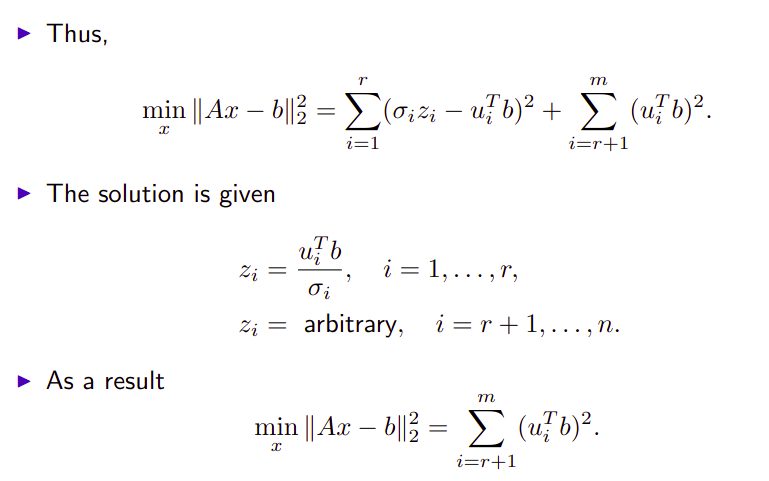
13.满秩分解

取自《矩阵论》 (opens new window)p179

设A为且秩为的复矩阵，记为，如果存在矩阵和，使得,则称为矩阵A的最大秩分解，满秩分解。

设，则一定存在和,使得

例如求矩阵A的满秩分解：

$$A=\left[\begin{array}{ccccc}1& 4& -1& 5& 6\\ 2& 0& 0& 4& 6\\ -1& 2& -4& -4& -19\\ 1& -2& -1& -1& -6\end{array}\right]$$

A进行初等行变换化为行标准形为：

$$A\simeq \left[\begin{array}{ccccc}1& 0& 0& 2& 3\\ 0& 1& 0& 1& 2\\ 0& 0& 1& 1& 5\\ 0& 0& 0& 0& 0\end{array}\right]$$

取A的前三列组成矩阵

$$B=\left[\begin{array}{ccc}1& 4& -1\\ 2& 0& 0\\ -1& 2& -4\\ 1& -2& -1\end{array}\right]$$

再取A的行标准形的前三个非零行，组成矩阵

$$C=\left[\begin{array}{ccccc}1& 0& 0& 2& 3\\ 0& 1& 0& 1& 2\\ 0& 0& 1& 1& 5\end{array}\right]$$

可以求得

14.Pseudo-Inverse Matrix

1920年摩尔提出广义逆的概念，1955年以4个方程的形式给出了广义逆矩阵的定义。
定义：设，若存在阶矩阵G，同时满足：

$$\begin{gathered} AGA=A \\ GAG=G \\ {(AG)}^T=AG \\ (GA{)}^T=GA \end{gathered}$$

则称G为A的加号逆，或伪逆，或摩尔彭斯逆(Moore–Penrose pseudoinverse),通常记为

对于任意,其伪逆存在且唯一。

伪逆的求法:

• (1)如果A为满秩方阵，则
• (2)如果,,则

$$\begin{gathered} A^{+}=diag(d_1^{+},d_2^{+},...d_n^{+}), \\ \mathrm{其}\mathrm{中},d_i^{+}=\{\begin{array}{c}0,d_i=0\mathrm{时}\\ \frac{1}{d_i},d_i\ne 0\mathrm{时}\end{array} \end{gathered}$$

• (3)如果A为行满秩矩阵，

$$A^{+}=A_R^{-1}=A^T(A{A}^T{)}^{-1}$$

• (4)如果A为列满秩矩阵，

$$A^{+}=A_L^{-1}=(A^{T}A{)}^{-1}{A}^T$$

• (5)如果A为降秩的矩阵，可用满秩分解求,即将A满秩分解为,其中B列满秩，C行满秩，且

$$rank(B)=rank(C)=r=rank(A)<minm,n,$$

则有：

$$A^{+}=C_R^{-1}{B}_L^{-1}=C^{+}{B}^{+}$$

这里：

$$B_L^{-1}=(B^{T}B{)}^{-1}{B}^T,C_R^{-1}=C^T(C{C}^T{)}^{-1}$$

from numpy import linalg as LA
import numpy as np
A = np.array([[1,1,0,1,0],[0,1,1,1,1],[1,0,1,1,0]])
LA.pinv(A)
"""output
array([[ 0.33333333, -0.33333333,  0.33333333],
       [ 0.5       ,  0.25      , -0.5       ],
       [-0.5       ,  0.25      ,  0.5       ],
       [ 0.16666667,  0.08333333,  0.16666667],
       [-0.16666667,  0.41666667, -0.16666667]])
"""

reference

• 1.https://zhuanlan.zhihu.com/p/50066691 (opens new window)
• 2.https://zhuanlan.zhihu.com/p/75060237 (opens new window)
• 3.https://zhuanlan.zhihu.com/p/103636446 (opens new window)